Definice
První Keplerův zákon určuje křivky, po níž se planety sluneční soustavy pohybují a zní následovně:
Planety se pohybují kolem Slunce po elipsách, málo odlišných od kružnic. Elipsy planet mají společné ohnisko, v němž se nachází Slunce. Druhá ohniska elips zůstávají prázdná.
Excentricity planet
Abychom si udělali představu toho, jak moc jsou elipsy, podél nichž se planety pohybují, podobné kružnicím, stačí se podívat na jejich relativní excentricity.
Největší relativní excentricitu má trajektorie planety Merkur, přibližně ε = 0,2. Trajektorie planet ve sluneční soustavě jsou tím pádem velmi málo protáhlé elipsy, které vypadají skoro jako kružnice.
Pojďme si na moment představit, že by elipsy planet měly větší relativní excentricitu, než doopravdy mají – elipsy by tak byly protáhlejší. I v tomto případě by Slunce stále zůstávalo v jejich společném ohnisku a zbylá ohniska nadále prázdná. Elipsy by mohly vypadat podle obrázku níže.
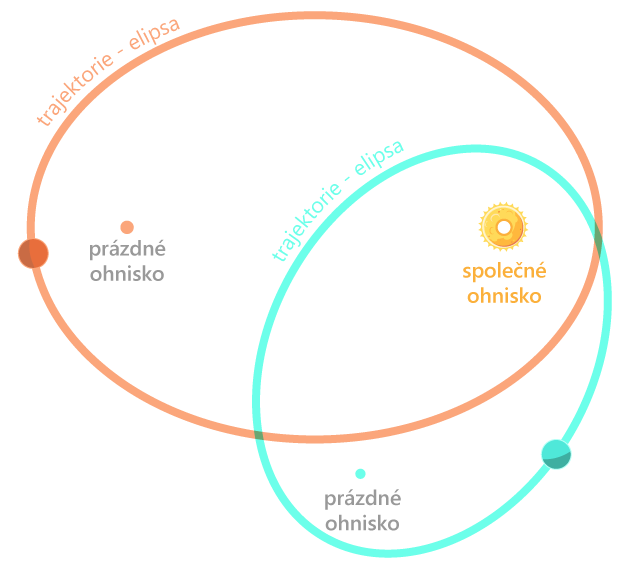
Perihélium a afélium
Bod elipsy, v němž se planeta nachází nejblíže ke Slunci, se nazývá perihélium (přísluní) a jeho vzdálenost od Slunce značíme rp.
Bod elipsy, v němž se planeta nachází naopak nejdále od Slunce, se nazývá afélium (odsluní) a jeho vzdálenost od Slunce značíme ra.
Vzdálenost k perihéliu snadno vyjádříme pomocí hlavní poloosy a (délkové) výstřednosti
$$ {r_p = a-e} $$Podobný vztah můžeme napsat pro vzdálenost afélia ke Slunci
$$ {r_a = a+e} $$Oběžná rovina
Z první Keplerova zákona plyne, že pohyb planet je rovinný, protože opisují elipsy. Elipsa je totiž křivka, která vždy leží v rovině.
Rovinu, v níž planeta obíhá Slunce, nazýváme oběžná rovina. Ta, ve které obíhá Země, má speciální jméno, rovina ekliptiky.
Oběžné roviny jsou pro různé planety obecně odlišné. Například Mars má jinou oběžnou rovinu než Země. I tak jsou ve skutečnosti oběžné roviny jednotlivých planet ve sluneční soustavě vůči sobě minimálně skloněné. Jak plyne z prvního Keplerova zákona, všechny tyto oběžné roviny mají Slunce jako svůj společný bod.
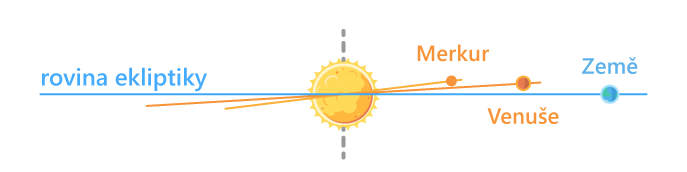
Sklon zemské osy a střídání ročních období
Nakonec přidejme jednu poznámku.
Zemský rovník svírá s rovinou ekliptiky úhel rovný přibližně 23,5°. Naklonění zemské osy vůči kolmici na rovinu ekliptiky má za následek střídání ročních období – v létě je severní polokoule Země osvětlena více než je v zimě.


